Normal function

In axiomatic set theory, a function f : Ord → Ord is called normal (or a normal function) iff it is continuous (with respect to the order topology) and strictly monotonically increasing. This is equivalent to the following two conditions:

1. For every limit ordinal γ (i.e. γ is neither zero nor a successor), f(γ) = sup {f(ν) : ν < γ}.
2. For all ordinals α < β, f(α) < f(β).

Contents 1 Examples 2 Properties 3 Notes 4 References

Examples

A simple normal function is given by f(α) = 1 + α; note however that f(α) = α + 1 is not normal. If β is a fixed ordinal, then the functions f(α) = β + α, f(α) = β × α and f(α) = β^α (for β > 1) are all normal.

More important examples of normal functions are given by the aleph numbers 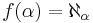which connect ordinal and cardinal numbers, and by the beth numbers .

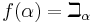Properties

If f is normal, then for any ordinal α,

f(α) ≥ α.^[1]

Proof: If not, choose γ minimal such that f(γ) < γ. Since f is strictly monotonically increasing, f(f(γ)) < f(γ), contradicting minimality of γ.

Furthermore, for any non-empty set S of ordinals, we have

f(sup S) = sup f(S).

Proof: "≥" follows from the monotonicity of f and the definition of the supremum. For "≤", set δ = sup S and consider three cases:

• if δ = 0, then S = {0} and sup f(S) = f(0);
• if δ = ν + 1 is a successor, then there exists s in S with ν < s, so that δ ≤ s. Therefore, f(δ) ≤ f(s), which implies f(δ) ≤ sup f(S);
• if δ is a nonzero limit, pick any ν < δ, and an s in S such that ν < s (possible since δ = sup S). Therefore f(ν) < f(s) so that f(ν) < sup f(S), yielding f(δ) = sup {f(ν) : ν < δ} ≤ sup f(S), as desired.

Every normal function f has arbitrarily large fixed points; see the fixed-point lemma for normal functions for a proof. One can create a normal function g : Ord → Ord, called the derivative of f, where g(α) is the α-th fixed point of f.^[2]

Notes

References

• Johnstone, Peter (1987), Notes on Logic and Set Theory, Cambridge University Press, ISBN 9780521336925 .